Relational Nature of Property Graphs
August 15, 2020
Marketing material about property graphs hides all the tradeoffs made to achieve their simplicity of use, they fail to give a fair comparison against the relational model. Even though the relational model has advantages over property graphs. I would even argue benefits of the relational model outweight those of property graphs.
SQL's popularity worked to its detriment. The increased visibility of SQL's shorfalls turned it into the web developer's scapegoat and banner for the no-SQL movement. From these alternative data models, property graphs seem to stand out. But, I think the property graphs are a regression over the relational data model.
Ed Codd himself, argued against graphs in the very first paper that introduced the idea of the relational model. Unfortunately his strongest arguments were against the tree data model, which was probably the most popular at the time. But, Trying to model the example in the paper as a property graph is a very good excercise to witness the data model's limitaitons.
The property graph data model doesn't require a schema upfront and offers an intuitive querying syntax. Both very good technical points against the relational's model abstract and mandatory schema, together with SQL's syntax, specially in the face of non-waterfall development processes. Still, I don't think property graphs should be more than just a convenient view on top of the relational model.
Diagrams of relational schemas have special notation for representing the relation's cardinality. Relational data is often mostly shown as tables with links. In contrast, the property graph model has direct visualizations as simple and intuitive diagrams. Because there's no schema, there's no huge need to visualize them, then data is just a graph with nodes and arrows. And even when schema diagrams become necessary, they can be generated and drawn again as just a graph. Unfortunately, this simpler visualization of data hides a lot of underlying tradeoffs.
I'll define a graphical notation that works for both relational and graph models. In doing so, I'll discuss some of the tradeoffs in the property graph model. I think a tool using this notation would offer the ease of use and simplicity of the property graph model, while not sacrificing any of the expressive power and granular control over space and time performance of the relational model.
Often property graphs and the relational data models use different vocabulary for equivalent concepts. The following is the generic word followed by the equivalent in the property graph and then in the relational model.
-
type: label, table
-
attribute: property, column
-
entities: node instance, rows
-
reference: edge instance, relation
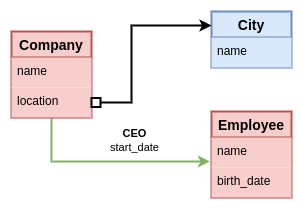
The following is a simple example of a SQL schema. It represents references as edges between the attributes involved the relation. The attribute where an entity's ID is defined is marked with a black port and the one storing the ID of the referenced entity is marked with a white port.
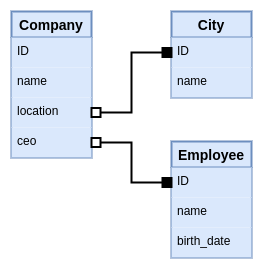
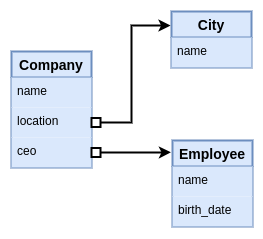
What happens if we want to store the date the CEO started acting in that position?. This is the kind of data that's not fully an attribute of the company, but also not of the employee. It belongs best to the relation between company and employee. This is a popular argument in favor of property graphs over the relational model, because you could have a graph as follows.
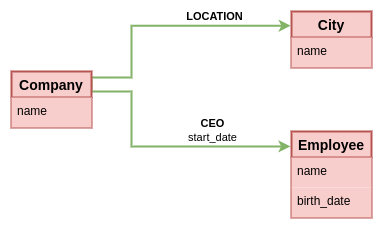
Something this notation doesn't convey, is the fact that the property graph model is creating an entity for these edges, and assigning a unique ID to them. It also uses a different syntax for edge properties than node properties, even though they are conceptually equivalent. Maybe a better notation that conveys the similarity of edges being attributed entities like nodes, would show an actual node between the edge.
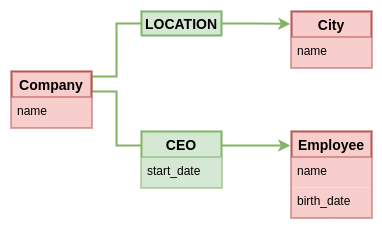
Even though this diagram may look simpler, often property graph implementations need to add some hidden infrastructure to support navigation through data. Specially to deliver on the promise of increased time performance while having consistent and predictable query execution time. We could show this internal plumbing using the relational notation from before. Here's one example of how that may look like.
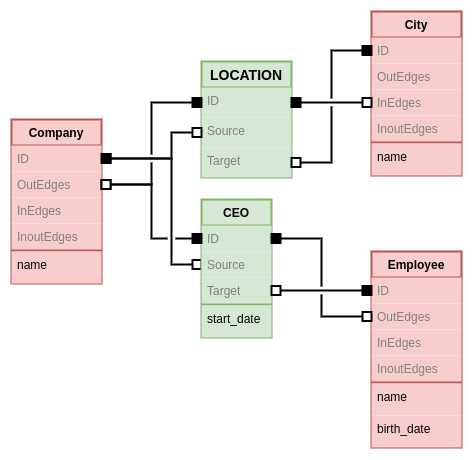
In truth, the original assumption about the relational model not supporting edge properties, is fundamentally wrong, that's preciseley the use for join tables. In fact join tables are even more generic in that they implement n-ary relationships efficiently, while the same in graph databases may lead to a quadratic explosion of the number of edge instances. In the relational model, the extended schema with the property in the edge would look as follows.
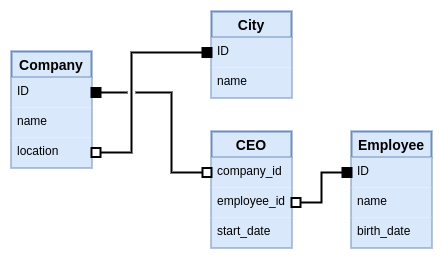
This is a nice balance which I think is more straightforward and truthful to the end user. It's right in between the extremes of the property graph diagrams which initially showed a very simple visualization, but then had an overy complex diagram when showing the underlying implementation hidden from the user.
This relational model has a few optimizations over the property graph one:
-
The location edge is implicit. Doesn't need a type and doesn't allocate IDs.
-
The rows in the CEO join table are uniqueley identified by its attributes. Again, avoiding the need of allocating and storing IDs for them.
A place where the property graph model may win might be in traversing a single edge. As a graph this a amounts to 2 sequential ID dereferences, assuming these are fast memory address references it could take constant time. In the relational model, a join would at best iterate once over each entry in the CEO table then perform a logarithmic indexed search to get the full result row. All this is time on the entries in the CEO table.
But, is the number of entries in the CEO table ever going to be so large to cause trouble?. Also, nothing guarantees that ID dereferences for a property graph implementation are constant time, they could be logarithmic searches on an index. So, is it really a clear and shut case which data model is faster here?, I think there are too many variables to know. Is it worth the extra space cost?.
It's clear that the relational approach offers a clear space advantage over the property graph one. So, how could we make this conceptually simpler and more approachable to users not familiar with the relational model?. Someone may argue the property graph implementation may be so good that it manages to be implented undernead as the relational model, but if that's the case, then what are the supposed benefits over the relational model?. It's unreasonable to argue for faster query time on the property graph model, if its underlying implementation is performing joins.
Implicit IDs
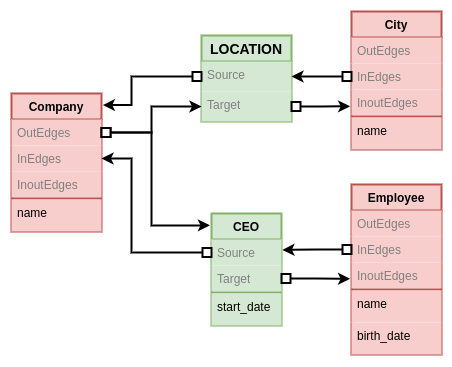
If we define the convention that types which have an ID field will always be represented as nodes, we don't need to show those attributes and we can replace the black ports with arrows pointing to any place around the node.
If we apply this to the complex drawing of the underlying implementation of the property graph model, we can see how this leads to a cleaner diagram. This is because it removes the restriction of positioning one edge end to a specific section in the node's border.
Best of Both Worlds
The best in the end is probably to mix both approaches. The color coding we've been using so far is good to distinguish between types implemented as relational tables and node/edge types that may contain hidden structure. We could leave the edge notation that doesn't use a node, to represent that this may not be an edge with an allocated ID itself, it may be implemented just by a join table. Assuming we keep the convention that entities with IDs are always represented as nodes.
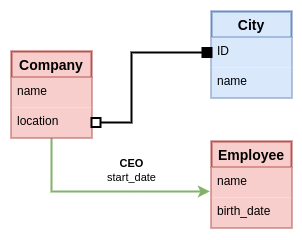
We could even go a step further with the assumption of nodes always having IDs and use the implicit ID notation.
Further Ideas
To me statements like "rleational model doesn't support edge properties", "property graphs are faster", "relational model is just property graphs without edges" are terribly misguided, so I've tried to counter them with "property graphs don't support implicit edges", "property graphs are larger" and "property graphs are just the relational model with join tables called edges". But that being said, I think instead of trying to argue which data model is better, we should try to understand the tradeoffs of each one and try to move further by attemtping to reconcile them.
What I would like is for the actual nuanced tradeoffs of data models to be studied and a system to be developed that is as friendly and easy to learn as property graphs, but offers the flexibility and control of the relational model.
Propery graph edges offer a more intuitive and easier to use conceptual framework for relational model's join tables. Yet, the relational model offers a clearer space and performance framework to reason about when developing a system.
For the mixed data model I described at the end, there are still some questions I wish I had good answers for:
-
How can we query the mixed data model in a way that is agnostic to changes from implicit edges becoming reified ones?.
-
What are all the possible optimization patterns that may be used when implementing a data model?
-
What are the time and space tradeoffs of each optimization pattern?
-
Is it possible to define an abstract data model where the implementation is free to apply any optimization pattern only when necessary?.